Menghitung radiasi matahari
Mata kuliah Mikrometeorologi membuat saya dan teman-teman melakukan pengamatan cuaca selama 24 jam di halaman Kampus IPB Baranangsiang, sangat menyenangkan karena waktu pengamatannya bertepatan dengan perayaan pergantian tahun 2003/2004.
Praktikum pengukuran profil iklim mikro fluks uap air dan bahang pada permukaan rumput
Tujuan dari praktikum ini adalah:
Menentukan variasi diurnal Radiasi netto (Rn) yang terdapat pada permukaan rumput
Mendapatkan variasi diurnal dari profil kecepatan angin, suhu udara, suhu tanah dan kelembaban spesifikpada permukaan rumput selama 24 jam.
Menentukan karakteristik kekasapan permukaan rumput (d, zo, dan U*)
Menetukan kondisi stabilitas atmosfer (Ri), netral, stabil dan inversi dalam periode 24 jam.
Menentukan besarnya energi yang digunakan untuk fluks bahang (QH) dan (QG), uap air (QE) pada kondisi netral.
Selain melakukan pengamatan, praktikum kali ini juga mengasah kemampuan saya dan teman-teman dalam menerapkan ilmu yang kita pelajari pada mata kuliah Instrumentasi Meteorologi untuk membuat beberapa IoT Anemometer portable dengan interface USB-2, sehingga data yang dihasilkan bisa langsung tersimpan di komputer untuk dianalisa lebih lanjut. Saya bertanggung jawab untuk mengamati Radiasi Netto, merekam data dan menganalisanya. Selain itu saya juga harus membandingkan dengan nilai dugaan Radiasi menggunakan pendekatan rumus empirik.
Slide di bawah ini adalah materi kuliah tentang radiasi matahari yang disampaikan Bu Tania June seminggu yang lalu, sebelum kita melakukan pengamatan lapangan.
Hasil pengamatan
Berdasarkan hasil praktikum terlihat adanya perubahan radiasi netto pada siang dan malam hari. Satuan miliVolt (mV) menunjukkan bahwa pengukuran radiasi netto ini menggunakan Net Radiometer dan DVM (Digital Volt Meter), diukur setiap 30 menit. Nilai Radiasi Netto pada siang hari ditunjukkan oleh grafik di bawah ini:
Selanjutnya saya harus membandingkan nilai radiasi hasil pengukuran dengan hasil dugaan menggunakan rumus empiris. Referensi saya adalah dokumen dari FAO no 56: Crop evapotranspiration - Guidelines for computing crop water requirements - FAO Irrigation and drainage paper 56 (http://www.fao.org/3/x0490e/x0490e00.htm#Contents): Chapter 3 yang membahas tentang data meteorologi, sub topik radiasi: http://www.fao.org/3/x0490e/x0490e07.htm#radiation
Menurut dokumen di atas, konsep dari perhitungan radiasi adalah sebagai berikut:
Radiasi ekstraterestrial (Ra)
Radiasi yang mengenai permukaan tegak lurus terhadap sinar matahari di bagian atas atmosfer bumi, yang disebut konstanta matahari, adalah sekitar 0,082 MJ m-2 mnt-1. Intensitas lokal radiasi ditentukan oleh sudut antara arah sinar matahari ke permukaan atmosfer. Sudut ini akan berubah pada siang hari dan akan berbeda di lintang yang berbeda dan di musim yang berbeda. Radiasi matahari yang diterima di bagian atas atmosfer bumi pada permukaan horizontal disebut radiasi ekstraterestrial, Ra. Jika matahari berada tepat di atas kepala, sudut datangnya nol dan radiasi ekstraterestrial 0,0820 MJ m-2 min-1. Saat musim berubah, posisi matahari dan panjang hari juga berubah, oleh karena itu Ra juga berubah. Radiasi ekstraterestrial dengan demikian merupakan fungsi dari garis lintang, tanggal dan waktu hari.
Ra untuk periode harian
Ra untuk periode harian dalam setahun dan untuk lintang yang berbeda dapat diperkirakan dari konstanta matahari, deklinasi matahari, dan waktu dalam setahun dengan:
Ra = (24(60))/π * Gsc * dr * [ωs * sin(φ) * sin(δ) + cos(φ) * cos(δ) * sin(ωs)] (Persamaan 1)
dimana :
Ra radiasi ekstraterestrial [MJ m-2 hari-1]
Gsc konstanta matahari = 0,0820 MJ m-2 menit-1
dr jarak relatif terbalik Bumi-Matahari (Persamaan 4)
ωs sudut waktu matahari terbenam, dalam radian (Persamaan 7 atau 8),
φ latitude, dalam radian (Persamaan 3)
δ sudut deklinasi matahari, dalam radian (Persamaan 5).
Dalam persamaan FAO Penman-Monteith tentang Evapotranspirasi, radiasi yang dinyatakan dalam MJ m-2 hari-1 dikonversi menjadi penguapan yang setara dalam mm hari-1 dengan menggunakan faktor konversi yang sama dengan kebalikan dari panas laten penguapan (1 / l = 0,408):
evaporasi [mm hari-1] = 0,408 x Radiasi [MJ m-2 hari-1] (Persamaan 2)
Ra diekspresikan dalam persamaan di atas dalam MJ m-2 hari-1. Penguapan dalam mm hari-1 diperoleh dengan mengalikan Ra dengan 0,408 (Persamaan 2). Garis lintang, φ, dinyatakan dalam radian positif untuk belahan bumi utara dan negatif untuk belahan selatan. Konversi dari derajat desimal ke radian diberikan oleh:
[Radians] = π/180 * [decimal degrees] (Persamaan 3)
Jarak relatif terbalik Bumi-Matahari, dr, dan deklinasi matahari, d, dihitung dari:
dr = 1 + 0.033 * cos(2π/365 * J) (Persamaan 4)
δ = 0.409 * sin(2π/365 * J - 1.39) (Persamaan 5)
dimana J adalah tanggal dalam Julian (https://landweb.modaps.eosdis.nasa.gov/browse/calendar.html), antara 1 (1 Januari) dan 365 atau 366 (31 Desember). J dapat ditentukan untuk setiap hari (D) bulan (M) melalui:
J = INTEGER (275 M / 9 - 30 + D) - 2
IF (M <3) THEN J = J + 2
IF (“tahun kabisat” and (M> 2)) THEN J = J + 1 (Persamaan 6)
Sudut waktu matahari terbenam, ωs, ditentukan dari:
ωs = arccos[-tan(φ) * tan(δ)] (Persamaan 7)
Karena fungsi arccos tidak tersedia dalam semua bahasa komputer, sudut waktu matahari terbenam juga dapat dihitung menggunakan fungsi arctan:
ωs = π/2 - arctan[(-tan(φ) * tan(δ))/X^0.5] (Persamaan 8)
dimana:
X = 1 - [tan(φ)]^2 [tan(δ)]^2 (Persamaan 9)
dan X = 0.00001 jika X ≤ 0
Ra untuk periode per jam atau yang lebih pendek
Untuk periode per jam atau lebih pendek, sudut waktu matahari pada awal dan akhir periode harus dipertimbangkan ketika menghitung Ra:
Ra = (12(60))/π * Gsc * dr * [(ω2 - ω1) * sin(φ) * sin(δ) + cos(φ) * cos(δ) * (sin(ω2)-sin(ω1))] (Persamaan 10)
dimana :
Ra radiasi ekstraterestrial per jam atau periode yang lebih pendek [MJ m-2 jam-1],
Gsc konstanta matahari = 0,0820 MJ m-2 menit-1,
dr jarak relatif terbalik Bumi-Matahari (Persamaan 4),
δ sudut deklinasi matahari, dalam radian (Persamaan 5),
φ latitude, dalam radian (Persamaan 3),
ω1 sudut waktu matahari terbit, dalam radian (Persamaan 11),
ω2 sudut waktu matahari terbenam, dalam radian (Persamaan 12),
Sudut waktu matahari terbit dan tenggelam dihitung menggunakan persamaan berikut:
ω1 = ω - (πt1/24) (Persamaan 11)
ω2 = ω + (πt1/24) (Persamaan 12)
dimana
ω sudut waktu matahari pada tengah hari atau periode lebih pendek, dalam radian,
t1 panjang periode perhitungan [jam]: misal. 1 untuk periode per jam atau 0,5 untuk periode 30 menit.
Sudut waktu matahari di titik tengah periode adalah:
ω = π/12 * [(t + 0.06667 * (Lz - Lm) + Sc) - 12] (Persamaan 13)
dimana
t waktu jam standar di tengah periode [jam]. Misalnya untuk periode antara 14.00 dan 15.00 jam, t = 14.5,
Lz lokasi bujur dari titik tengah dari zona waktu lokal [derajat Bujur Barat Greenwich]. Misalnya, Lz = 75, 90, 105 dan 120° untuk zona waktu wilayah Timur, Tengah, Pegunungan Rocky dan Pasifik (Amerika Serikat) dan Lz = 0° untuk Greenwich, 330° untuk Kairo (Mesir), dan 255° untuk Bangkok (Thailand),
Lm bujur dari lokasi pengukuran [derajat Bujur Barat Greenwich],
Sc Koreksi musiman untuk waktu matahari [jam].
Tentu saja, jika w < -ws atau w > ws dari Persamaan 13 menunjukkan bahwa matahari berada di bawah cakrawala sehingga, menurut definisi, Ra adalah nol.
Koreksi musiman untuk waktu matahari adalah:
Sc = 0.1645 * sin(2 b) - 0.1255 * cos(b) - 0.025 sin(b) (Persamaan 14)
b = (2π(J-81))/364 (Persamaan 15)
dimana J adalah hari ke-n dalam setahun.
Lama penyinaran, dalam jam (N)
Dihitung menggunakan persamaan berikut:
N = 24/π * ωs (Persamaan 16)
di mana ωs adalah sudut waktu matahari terbenam dalam radian yang diberikan oleh Persamaan 7 atau 8.
Radiasi matahari (Rs)
Jika radiasi matahari, Rs, tidak terukur, dapat dihitung dengan rumus Angstrom yang menghubungkan radiasi matahari dengan radiasi ekstraterestrial dan durasi sinar matahari relatif:
Rs = (as + bs * (n/N)) * Ra (Persamaan 17)
dimana
Rs radiasi matahari atau gelombang pendek [MJ m-2 hari-1],
n durasi aktual sinar matahari [jam],
N durasi maksimum yang mungkin dari sinar matahari atau panjang hari [jam],
n/N durasi sinar matahari relatif [-],
Ra radiasi ekstarterrestrial [MJ m-2 hari-1],
as sebagai konstanta regresi, menyatakan fraksi radiasi ekstraterestrial yang mencapai bumi pada hari-hari mendung (n = 0),
as+bs sebagai fraksi radiasi ekstraterestrial yang mencapai bumi pada hari-hari cerah (n = N).
Rs dinyatakan dalam persamaan di atas dalam MJ m-2 hari-1. Penguapan setara yang sesuai dalam mm hari-1 diperoleh dengan mengalikan Rs dengan 0,408 (Persamaan 2). Bergantung pada kondisi atmosfer (kelembaban, debu) dan deklinasi matahari (garis lintang dan bulan), nilai Angstrom as dan bs akan bervariasi. Ketika tidak ada data radiasi matahari aktual yang tersedia dan tidak ada kalibrasi telah dilakukan untuk parameter as dan bs yang ditingkatkan, nilai yang direkomendasikan untuk as = 0,25 dan bs = 0,50.
Radiasi ekstraterestrial, Ra, dan panjang hari atau durasi maksimum yang mungkin dari sinar matahari, N, diberikan oleh Persamaan 10 dan 16. Durasi aktual sinar matahari, n, direkam dengan perekam sinar matahari Campbell Stokes.
Radiasi matahari, ketika langit cerah (Rso)
Perhitungan radiasi ketika langit-cerah, Rso, ketika n = N, diperlukan untuk menghitung radiasi gelombang panjang netto.
Untuk dekat permukaan laut atau ketika nilai kalibrasi untuk as dan bs tersedia:
Rso = (as + bs) Ra (Persamaan 18)
dimana
Rso radiasi matahari ketika langit cerah [MJ m-2 hari-1],
as + bs fraksi radiasi ekstraterestrial yang mencapai bumi pada hari-hari langit cerah (n = N).
Ketika nilai kalibrasi untuk as dan bs tidak tersedia:
Rso = (0,75 + 2E10-5z) Ra (Persamaan 19)
dimana
z ketinggian stasiun di atas permukaan laut [m].
Radiasi matahari atau gelombang pendek netto (Rns)
Radiasi gelombang pendek netto yang dihasilkan dari keseimbangan antara radiasi matahari yang masuk dan yang dipantulkan diberikan oleh:
Rns = (1-a) Rs (Persamaan 20)
dimana
Rns radiasi matahari atau gelombang pendek netto [MJ m-2 hari-1],
a koefisien refleksi albedo atau kanopi, yang bernilai 0.23 untuk referensi hipotesis tanaman rumput [tidak mempunyai unit],
Rs radiasi matahari yang masuk [MJ m-2 hari-1].
Radiasi gelombang panjang netto (Rnl)
Tingkat emisi energi gelombang panjang sebanding dengan suhu absolut permukaan yang dipangkatkan empat. Hubungan ini diekspresikan secara kuantitatif oleh hukum Stefan-Boltzmann. Namun, fluks energi bersih yang meninggalkan permukaan bumi kurang dari yang dipancarkan dan diberikan oleh hukum Stefan-Boltzmann karena penyerapan dan radiasi ke bawah dari langit. Uap air, awan, karbon dioksida, dan debu adalah penyerap dan penghasil radiasi gelombang panjang. Konsentrasi mereka harus diketahui ketika menilai fluks keluar netto. Karena kelembaban dan kekeruhan memainkan peran penting, hukum Stefan-Boltzmann dikoreksi oleh dua faktor ini ketika memperkirakan - fluks keluar radiasi gelombang panjang. Dengan demikian diasumsikan bahwa konsentrasi peredam lain adalah konstan:
Rnl = σ[((Tmax + 273.16)^4 + (Tmin + 273.16)^4) / 2] * (0.34 - 0.14√ea) * [1.35 * Rs/Rso - 0.35] (Persamaan 21)
dimana
Rnl radiasi gelombang panjang keluar netto [MJ m-2 hari-1],
σ Konstanta Stefan-Boltzmann [4,903 10-9 MJ K-4 m-2 hari-1],
Tmax, dalam Kelvin, suhu absolut maksimum selama periode 24 jam [K = °C + 273,16],
Tmin, dalam Kelvin, suhu absolut minimum selama periode 24 jam [K = °C + 273,16],
ea tekanan uap aktual [kPa],
Rs/Rso Radiasi gelombang pendek relatif (terbatas pada ≤ 1.0),
Rs dihitung dari (Persamaan 17) radiasi matahari [MJ m-2 hari-1],
Rso dihitung dari (Persamaan 18 atau 19) radiasi langit cerah [MJ m-2 hari-1].
Rata-rata suhu udara maksimum dan suhu udara minimum yang dipangkatkan empat biasanya digunakan dalam persamaan Stefan-Boltzmann untuk periode waktu 24 jam. Istilah (0.34-0.14√ea) menyatakan koreksi untuk kelembaban udara, dan akan lebih kecil jika kelembaban meningkat. Efek kekeruhan diungkapkan oleh (1.35 Rs / Rso - 0.35). Istilah ini menjadi lebih kecil jika kekeruhan meningkat dan karenanya Rs berkurang. Semakin kecil ketentuan koreksi, semakin kecil fluks keluar radiasi gelombang panjang. Perhatikan bahwa istilah Rs/Rso dalam Persamaan 39 harus dibatasi sehingga Rs / Rso ≤ 1.0.
Di mana pengukuran radiasi pendek dan gelombang panjang masuk dan keluar selama langit cerah dan mendung tersedia, kalibrasi koefisien dalam Persamaan 39 dapat dilakukan.
Radiasi netto (Rn)
Radiasi netto (Rn) adalah perbedaan antara radiasi gelombang pendek netto masuk (Rns) dan radiasi gelombang panjang netto keluar (Rnl):
Rn = Rns - Rnl (Persamaan 22)
Script menggunakan bahasa BASIC
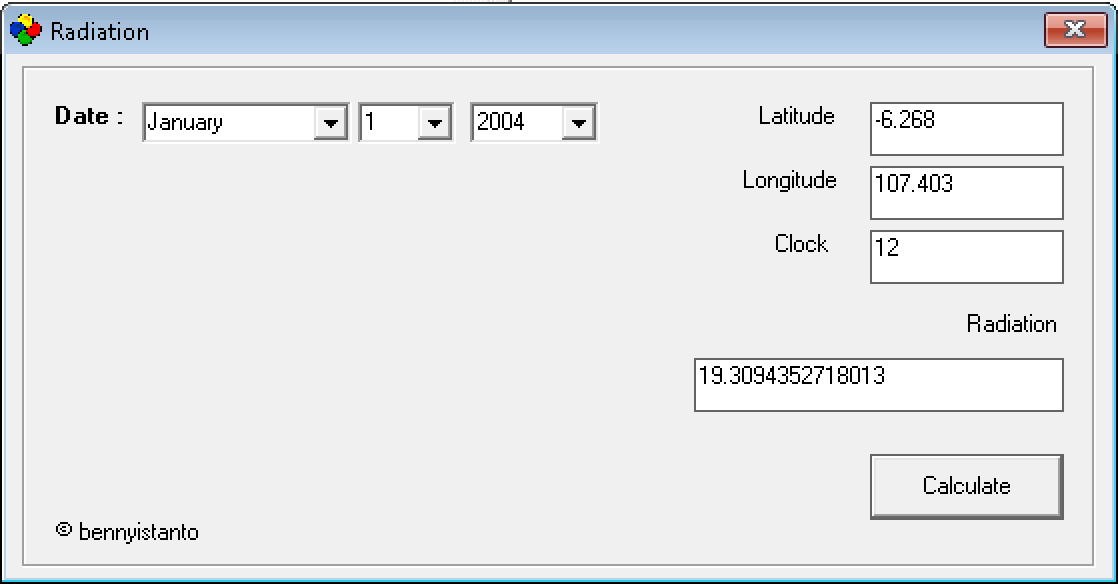
Selanjutnya untuk memudahkan perhitungan radiasi harian selama 1 tahun, beberapa persamaan diatas saya tulis menggunakan bahasa BASIC (kodenya dapat dilihat dibagian bawah tulisan). Dan untuk perhitungan 1 waktu, saya buat user interface sederhana menggunakan Visual Basic 6 seperti gambar dibawah.
Gambar 1. UI program menghitung radiasi matahari.
'++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
' Program untuk menghitung Radiasi
' Benny Istanto, G241010143
' Praktikum matakuliah Mikrometeorologi, Semester 5
' 1 Jan 2004, Lapangan Taman Koleksi - Kampus IPB Baranangsiang
' Referensi: http://www.fao.org/3/x0490e/x0490e07.htm#radiation
'++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
'Pengenal variabel
'Rs = rata-rata bulanan radiasi global harian yang jatuh pada permukaan horizontal [MJ m-2 hari-1]
'Ra = radiasi ekstraterestrial (radiasi yang sampai di puncak atmosfer/radiasi angot) harian yang
' jatuh pada permukaan horizontal tiap satuan luas [MJ m-2 hari-1]
'ax + bx = fraksi radiasi ekstraterestrial yang sampai ke bumi pada hari cerah
'n = lama penyinaran
'nMax = lama penyinaran harian maksimum (pada hari cerah) [jam]
'Gsc = konstanta matahari
'dr = inverse jarak bumi - matahari [Radian]
'Ws = sudut matahari terbenam [Radian]
'W = lintang [Radian]
'dekl = sudut deklinasi [Radian]
Dim g%, z%, rads, Rs, Ra, ax, bx, n, nMax, Gsc, dr, Ws
Dim Lat, W, dekl, pi, sinld, cosld, sinb, arg, arccos
Dim Tahun, Day, X, W1, W2, WW, Lz, Lm, Sc, b, t, MONTH, hari
'+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
'Calculate Julian Date
'+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Dim bulan(20), bfeb As Integer
bulan(1) = 31
'Bulan kabisat
If Val(frmRadiation.cboTahun.Text) Mod 4 = 0 Then bfeb = 29 Else bfeb = 28
bulan(2) = bulan(1): bulan(3) = bulan(2) + bfeb: bulan(4) = bulan(3) + 31
bulan(5) = bulan(4) + 30: bulan(6) = bulan(5) + 31: bulan(7) = bulan(6) + 30
bulan(8) = bulan(7) + 31: bulan(9) = bulan(8) + 31: bulan(10) = bulan(9) + 30
bulan(11) = bulan(10) + 31: bulan(12) = bulan(11) + 30
'Isi Combo box
With cboBulan
If .Text = "January" Then MONTH = 0
If .Text = "February" Then MONTH = 1
If .Text = "March" Then MONTH = 2
If .Text = "April" Then MONTH = 3
If .Text = "May" Then MONTH = 4
If .Text = "June" Then MONTH = 5
If .Text = "July" Then MONTH = 6
If .Text = "August" Then MONTH = 7
If .Text = "September" Then MONTH = 8
If .Text = "October" Then MONTH = 9
If .Text = "November" Then MONTH = 10
If .Text = "December" Then MONTH = 11
End With
If MONTH = 0 Then
JulianDate = Val(frmRadiation.cboTanggal.Text)
Else
JulianDate = bulan(MONTH) + Val(frmRadiation.cboTanggal.Text)
End If
'+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Open App.Path & "\Book1.csv" For Input As 1
Open App.Path & "\Book2.csv" For Output As 2
g% = 0
While Not EOF(1)
g% = g% + 1
jumlah = g%
For z% = 1 To jumlah
Input #1, dino(g%)
Day = dino(g%)
ax = 0.25
bx = 0.5
Lat = txtLat.Text
Gsc = 0.082
pi = 3.14159265358979
Lz = 255
Lm = txtLon.Text
t = txtClock.Text
W = (pi / 180) * Lat
dr = 1 + (0.033 * (Cos(((2 * pi) / 365) * Day)))
dekl = 0.409 * (Sin((((2 * pi) / 365) * Day) - 1.39))
X = 1 - (((Tan(W)) ^ 2) * ((Tan(dekl)) ^ 2))
If X <= 0 Then X = 0.00001
Ws = (pi / 2) - (arctan * ((((-Tan(W)) * (Tan(dekl))) / (X ^ 0.5))))
n = 7.1
nMax = (24 / pi) * dekl
b = ((2 * pi) * (Day - 81)) / 364
Sc = (0.1645 * (Sin(2 * b))) - (0.1255 * (Cos(b))) - (0.025 * (Sin(b)))
WW = (pi / 12) * ((t + (0.06667 * (Lz - Lm)) + Sc) - 12)
W1 = WW - ((pi * 0.5) / 24)
W2 = WW + ((pi * 0.5) / 24)
Ra = ((12 * 60) / pi) * Gsc * dr * ((((W2 - W1) * (Sin(W)) * (Sin(dekl))) + _
((Cos(W)) * (Cos(dekl)) * ((Sin(W2) - (Sin(W1)))))))
Rs = (ax + (bx * (n / nMax))) * Ra
txtRad.Text = Rs * 11.6
rads = Rs * 11.6
Write #2, Day, rads
Next z%
Wend
Close #1
MsgBox "complete"